回帰分析を極める(1/4):重回帰分析

回帰分析は統計学の中でも最も基本的で重要な手法の一つです。本シリーズでは、回帰分析の理論から実装まで、4回にわたって詳しく解説していきます。第1回目となる今回は、重回帰分析の基礎から正則化手法まで幅広く取り上げます。
重回帰分析とは
重回帰分析は、複数の説明変数を用いて目的変数を予測・説明する統計手法です。一般的な重回帰モデルは以下のように表現されます:
\[y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_p x_p + \varepsilon\]
ここで、\(y\)は目的変数、\(x_1, x_2, \ldots, x_p\)は説明変数、\(\beta_0, \beta_1, \ldots, \beta_p\)は回帰係数、\(\varepsilon\)は誤差項です。
最小2乗法
回帰係数の推定には最小2乗法が一般的に用いられます。これは残差平方和を最小化することで係数を求める手法です。
残差平方和は以下のように定義されます:
\[RSS = \sum_{i=1}^{n} (y_i – \hat{y}_i)^2 = \sum_{i=1}^{n} (y_i – \beta_0 – \beta_1 x_{i1} – \cdots – \beta_p x_{ip})^2\]
行列表記を用いると、回帰係数の最小2乗推定量は以下のようになります。
\[\hat{\boldsymbol{\beta}} = (\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y}\]
モデル評価指標
決定係数
決定係数(\(R^2\))は、モデルがデータの変動をどの程度説明できているかを表す指標です:
\[R^2 = 1 – \frac{RSS}{TSS} = 1 – \frac{\sum_{i=1}^{n}(y_i – \hat{y}_i)^2}{\sum_{i=1}^{n}(y_i – \bar{y})^2}\]
自由度調整済み決定係数
決定係数は説明変数を増やすと必ず増加するため、モデル比較には自由度調整済み決定係数が用いられます:
\[R_{adj}^2 = 1 – \frac{RSS/(n-p-1)}{TSS/(n-1)}\]
正則化
高次元データや多重共線性の問題に対処するため、正則化手法が用いられます。正則化は、回帰係数にペナルティを課すことで過学習を防ぎます。
L2正則化(リッジ回帰)
L2正則化(リッジ回帰)では、回帰係数の二乗和にペナルティを課します:
$$\min_{\boldsymbol{\beta}} |\boldsymbol{y} – \boldsymbol{X}\boldsymbol{\beta}|^2 + \lambda |\boldsymbol{\beta}|_2^2$$
L1正則化(Lasso回帰)
L1正則化(Lasso回帰)では、回帰係数の絶対値の和にペナルティを課します:
$$\min_{\boldsymbol{\beta}} |\boldsymbol{y} – \boldsymbol{X}\boldsymbol{\beta}|^2 + \lambda |\boldsymbol{\beta}|_1$$
Lasso回帰は変数選択機能を持ち、一部の回帰係数を正確に0にします。
Elastic Net
Elastic Netは、L1正則化とL2正則化を組み合わせた手法です:
$$\min_{\boldsymbol{\beta}} |\boldsymbol{y} – \boldsymbol{X}\boldsymbol{\beta}|^2 + \lambda [(1-\alpha)|\boldsymbol{\beta}|_2^2 + \alpha|\boldsymbol{\beta}|_1]$$
Rによる実装:正則化パス
以下では、glmnetパッケージを用いて正則化パスを可視化します。正則化パスとは、正則化パラメータ$\lambda$を変化させたときの回帰係数の変化を可視化したものです。これにより、どの変数がどの程度の正則化で除去されるかを理解できます。なお、データセットとして、Boston住宅価格データを使用しています。
# 必要なライブラリの読み込み
library(glmnet)
library(MASS)
# Boston住宅価格データの準備
data(Boston)
X <- as.matrix(Boston[, -14]) # medvを除く
y <- Boston$medv
X_scaled <- scale(X) # データの標準化
# 正則化パスの計算
ridge_fit <- glmnet(X_scaled, y, alpha = 0, lambda = exp(seq(5, -5, length.out = 100)))
lasso_fit <- glmnet(X_scaled, y, alpha = 1, lambda = exp(seq(2, -5, length.out = 100)))
elastic_fit <- glmnet(X_scaled, y, alpha = 0.5, lambda = exp(seq(2, -5, length.out = 100)))
# 正則化パスの可視化(余白を調整)
par(mfrow = c(2, 2), mar = c(4, 4, 5.5, 2), oma = c(1, 1, 1, 1))
# 1. リッジ回帰パス
plot(ridge_fit, xvar = "lambda", label = TRUE, main = "Ridge Regression Path")
# 2. Lasso回帰パス
plot(lasso_fit, xvar = "lambda", label = TRUE, main = "Lasso Regression Path")
# 3. Elastic Net パス
plot(elastic_fit, xvar = "lambda", label = TRUE, main = "Elastic Net Path (α=0.5)")
# 4. 交差検証結果(Lasso)
cv_lasso <- cv.glmnet(X_scaled, y, alpha = 1)
plot(cv_lasso, main = "Lasso Cross-Validation")
abline(v = log(cv_lasso$lambda.min), col = "red", lty = 2)
abline(v = log(cv_lasso$lambda.1se), col = "blue", lty = 2)
# 結果の表示
cat("最適lambda値:\\n")
cat("Lasso lambda.min:", cv_lasso$lambda.min, "\\n")
cat("Lasso lambda.1se:", cv_lasso$lambda.1se, "\\n")
# 最適パラメータでの係数
coef_lasso <- as.vector(coef(cv_lasso, s = cv_lasso$lambda.min))
coef_names <- rownames(coef(cv_lasso, s = cv_lasso$lambda.min))
# 非ゼロ係数の抽出
nonzero_idx <- which(coef_lasso != 0)
nonzero_coef <- data.frame(
Variable = coef_names[nonzero_idx],
Coefficient = coef_lasso[nonzero_idx]
)
cat("\\nLassoの非ゼロ係数:\\n")
print(nonzero_coef)出力結果
最適lambda値:
Lasso lambda.min: 0.02800535
Lasso lambda.1se: 0.4158705
Lassoの非ゼロ係数:
Variable Coefficient
1 (Intercept) 22.5328063
2 crim -0.8459305
3 zn 0.9665200
4 chas 0.6820217
5 nox -1.8895761
6 rm 2.7169775
7 dis -2.9396168
8 rad 2.2002069
9 tax -1.6561804
10 ptratio -2.0133748
11 black 0.8240161
12 lstat -3.7312035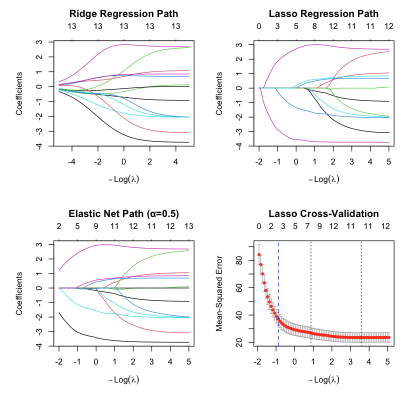
正則化パスの解釈
作成された4つのプロットから以下のことが分かります:
- Ridge Regression Path: リッジ回帰では係数は0に近づきますが、完全には0になりません
- Lasso Regression Path: Lasso回帰では多くの係数が正確に0になり、変数選択が行われます
- Elastic Net Path: L1とL2の中間的な性質を示し、段階的に変数が除去されます
- 交差検証結果: 最適なλ値を客観的に選択できます
まとめ
本記事では、重回帰分析の基礎から正則化手法まで解説し、実際のRコードで正則化パスを可視化しました。重要なポイントは以下の通りです。
- 最小2乗法は回帰係数推定の基本手法
- 決定係数でモデル性能を評価
- 正則化により過学習と多重共線性の問題を解決
- L1正則化は変数選択、L2正則化は係数の安定化に有効
- 正則化パスにより最適なパラメータを視覚的に理解
次回は回帰診断法について詳しく解説し、モデルの妥当性を検証する手法を学びます。




