回帰分析を極める(2/4):回帰診断法

前回は重回帰分析の基礎理論と正則化手法について学びました。今回は、構築した回帰モデルが適切かどうかを診断する手法について詳しく解説します。回帰診断は、モデルの前提条件の確認や外れ値・影響点の検出において極めて重要です。
目次
回帰診断の重要性
回帰分析では以下の前提条件が仮定されています:
- 線形性: 説明変数と目的変数の関係が線形
- 独立性: 観測値が互いに独立
- 等分散性: 誤差項の分散が一定
- 正規性: 誤差項が正規分布に従う
これらの前提条件が満たされない場合、推定結果の信頼性が損なわれます。回帰診断により、これらの問題を検出し、適切な対処法を検討することができます。
残差の種類
回帰診断では様々な種類の残差を用います:
通常の残差
\[e_i = y_i – \hat{y}_i\]
標準化残差
\[r_i = \frac{e_i}{\hat{\sigma}\sqrt{1-h_{ii}}}\]
スチューデント化残差
\[t_i = \frac{e_i}{\hat{\sigma}_{(i)}\sqrt{1-h_{ii}}}\]
ここで、\(\hat{\sigma}_{(i)}\)は\(i\)番目の観測値を除いて計算した誤差の標準偏差、\(h_{ii}\)はてこ比です。
残差プロット
残差プロットは、回帰診断において最も基本的で重要な手法です。様々な残差プロットにより、異なる問題を検出できます。
残差 vs 予測値プロット
残差と予測値の散布図により、以下を確認できます:
- 等分散性: 点がランダムに散らばっているか
- 線形性: 明確なパターンがないか
- 外れ値: 他の点から大きく外れた点がないか
理想的には、点が水平線(y=0)の周りにランダムに散らばっているべきです。
正規Q-Qプロット
正規Q-Qプロット(Quantile-Quantile plot)は、残差の正規性を視覚的に確認する手法です。
理論的には、残差が正規分布に従う場合、Q-Qプロットの点は直線上に並びます。正規分布からの逸脱は以下のパターンで現れます:
- S字型カーブ: 分布が厚い裾を持つ
- 逆S字型カーブ: 分布が薄い裾を持つ
- 上に凸の曲線: 右に歪んだ分布
- 下に凸の曲線: 左に歪んだ分布
てこ比
てこ比(leverage)\(h_{ii}\)は、\(i\)番目の観測値が予測値に与える影響の大きさを表します:
\[h_{ii} = \boldsymbol{x}_i^T(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{x}_i\]
てこ比の性質:
- \(0 \leq h_{ii} \leq 1\)
- \(\sum_{i=1}^{n} h_{ii} = p+1\)(\(p\)は説明変数の数)
- 高いてこ比の観測値は、説明変数空間で外れた位置にある
一般的に、\(h_{ii} > \frac{2(p+1)}{n}\)の観測値は高いてこ比を持つとされます。
Cookの距離
Cookの距離\(D_i\)は、\(i\)番目の観測値がすべての予測値に与える影響を測定します:
\[D_i = \frac{r_i^2}{p+1} \cdot \frac{h_{ii}}{1-h_{ii}}\]
または、予測値の変化量として:
\[D_i = \frac{(\hat{\boldsymbol{y}} – \hat{\boldsymbol{y}}_{(i)})^T(\hat{\boldsymbol{y}} – \hat{\boldsymbol{y}}_{(i)})}{(p+1)\hat{\sigma}^2}\]
一般的に、\(D_i > \frac{4}{n}\)または\(D_i > 1\)の観測値は影響点とされます。
診断の手順
- 残差プロットで基本的な前提条件を確認
- 正規Q-Qプロットで正規性を確認
- てこ比で説明変数空間の外れ値を検出
- Cookの距離で影響点を特定
- 問題のある観測値について詳細に調査
- 必要に応じてモデルの修正や再分析を実施
Rによる実装:残差プロットと正規Q-Qプロット
以下では、様々な回帰診断手法をRで実装します。なお、データセットとして、Boston住宅価格データを使用しています。
# データの準備
library(MASS)
data(Boston)
# 重回帰モデルの構築
model <- lm(medv ~ ., data = Boston)
# 診断統計量の計算
residuals <- residuals(model)
fitted <- fitted(model)
std_residuals <- rstandard(model)
cooks_dist <- cooks.distance(model)
# 回帰診断プロット
par(mfrow = c(2, 2), mar = c(4, 4, 3, 2))
# 1. 残差 vs 予測値
plot(fitted, residuals, main = "Residuals vs Fitted",
xlab = "Fitted Values", ylab = "Residuals", pch = 16)
abline(h = 0, col = "red", lty = 2)
# 2. 正規Q-Qプロット
qqnorm(std_residuals, main = "Normal Q-Q Plot", pch = 16)
qqline(std_residuals, col = "red", lwd = 2)
# 3. スケール-ロケーションプロット
plot(fitted, sqrt(abs(std_residuals)), main = "Scale-Location",
xlab = "Fitted Values", ylab = "√|Standardized Residuals|", pch = 16)
# 4. Cookの距離
plot(1:length(cooks_dist), cooks_dist, type = "h",
main = "Cook's Distance", xlab = "Observation", ylab = "Cook's Distance")
abline(h = 4/length(cooks_dist), col = "red", lty = 2)
# 影響点の特定
influential <- which(cooks_dist > 4/length(cooks_dist))
cat("影響点の観測値番号:", influential, "\\n")
cat("影響点の数:", length(influential), "\\n")
出力結果
影響点の観測値番号: 65 142 149 162 163 164 167 187 196 205 215 226 229 234 254 263 268 365 366 368 369 370 371 372 373 375 376 381 413 415
影響点の数: 30
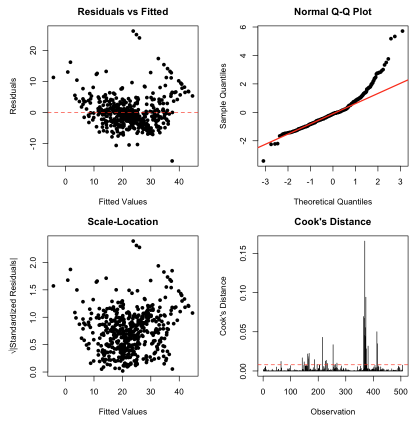
出力結果の解釈
作成される4つの診断プロットはそれぞれ以下を確認するときに使われます:
- Residuals vs Fitted: 線形性と等分散性の確認
- Normal Q-Q Plot: 残差の正規性の確認
- Scale-Location: 等分散性の詳細な確認
- Cook’s Distance: 影響点の特定
これらを踏まえると、以下のような診断が可能です:
残差プロットから分かること
- 等分散性: スケール-ロケーションプロットで水平線が理想的
- 線形性: 残差vs予測値プロットでパターンがないことが理想的
- 外れ値: 標準化残差が±2を超える点
正規Q-Qプロットから分かること
- 点が直線に沿っていれば正規性が満たされている
- S字型や逆S字型のパターンは分布の歪みを示す
影響点診断から分かること
- 高いてこ比: 説明変数空間で外れた観測値
- 高いCookの距離: 予測に大きな影響を与える観測値
まとめ
回帰診断は回帰分析において極めて重要なプロセスです。本記事で学んだポイントは次のとおりです:
- 残差プロットで基本的な前提条件を視覚的に確認
- 正規Q-Qプロットで残差の正規性を評価
- てこ比で説明変数空間の外れ値を検出
- Cookの距離で予測に影響を与える観測値を特定
- 統計的検定で客観的な評価を実施
- 問題が発見された場合の対処法を検討
適切な回帰診断により、信頼性の高い回帰モデルを構築することができます。次回は質的回帰について学び、カテゴリカルな目的変数を扱う手法を探求します。

