回帰分析を極める(4/4):回帰分析その他

回帰分析シリーズの最終回となる今回は、特殊な応用分野における回帰手法について解説します。制限付き従属変数を扱うトービットモデル、時間軸を考慮した生存時間分析、そして現代の機械学習の代表格であるニューラルネットワークモデルまで、幅広い回帰分析の応用を学びます。
目次
トービットモデル
トービットモデル(Tobit Model)は、目的変数が特定の値で切断される(censored)データを扱う回帰モデルです。1958年にJames Tobinによって提案されました。
モデルの定式化
潜在変数\(y_i^*\)があり、実際に観測される\(y_i\)は:
\[y_i = \begin{cases} y_i^* & \text{if } y_i^* > 0 \\ 0 & \text{if } y_i^* \leq 0 \end{cases}\]
潜在変数は線形回帰モデルに従います:
\[y_i^* = \boldsymbol{x}_i^T\boldsymbol{\beta} + \varepsilon_i, \quad \varepsilon_i \sim N(0, \sigma^2)\]
応用例
- 消費支出: 負の支出は観測されない
- 労働時間: 0時間未満は観測されない
- 投資額: 負の投資は観測されない
推定方法
最尤推定を用います。尤度関数は:
\[L = \prod_{y_i=0} P(y_i^* \leq 0) \prod_{y_i>0} f(y_i)\]
ここで、\(P(y_i^* \leq 0) = \Phi(-\boldsymbol{x}_i^T\boldsymbol{\beta}/\sigma)\)、\(f(y_i)\)は切断されていない観測値の密度関数です。
生存時間分析
生存時間分析(Survival Analysis)は、ある事象(死亡、再発、故障など)が発生するまでの時間を分析する統計手法です。
基本概念
生存時間
事象発生までの時間\(T\)。通常は非負の連続変数です。
打ち切り(Censoring)
観察期間中に事象が発生しない場合、真の生存時間は未知となります。これを打ち切りと呼びます。
主な打ち切りの種類:
- 右打ち切り: 観察終了時点で事象未発生
- 左打ち切り: 観察開始前に事象発生の可能性
- 区間打ち切り: 事象発生時刻が区間内で不明
生存関数
生存関数\(S(t)\)は、時刻\(t\)まで事象が発生しない確率です:
\[S(t) = P(T > t) = 1 – F(t)\]
ここで、\(F(t)\)は累積分布関数です。
生存関数の性質:
- \(S(0) = 1\)
- \(S(\infty) = 0\)
- 単調非増加関数
ハザード関数
ハザード関数\(h(t)\)は、時刻\(t\)まで生存した条件下での瞬間死亡率です:
\[h(t) = \lim_{\Delta t \to 0} \frac{P(t \leq T < t + \Delta t | T \geq t)}{\Delta t}\]
これは以下のようにも表現されます:
\[h(t) = \frac{f(t)}{S(t)} = -\frac{d}{dt}\log S(t)\]
累積ハザード関数
累積ハザード関数\(H(t)\)は、ハザード関数の積分です:
\[H(t) = \int_0^t h(u) du = -\log S(t)\]
これにより、生存関数は:
\[S(t) = \exp(-H(t))\]
カプラン・マイヤー法
カプラン・マイヤー法(Kaplan-Meier method)は、打ち切りデータがある場合の生存関数のノンパラメトリック推定法です。
カプラン・マイヤー推定量
事象発生時刻を\(t_1 < t_2 < \cdots < t_k\)とするとき、カプラン・マイヤー推定量は:
\[\hat{S}(t) = \prod_{t_i \leq t} \left(1 – \frac{d_i}{n_i}\right)\]
ここで:
- \(d_i\): 時刻\(t_i\)での事象発生数
- \(n_i\): 時刻\(t_i\)直前のリスク集合の大きさ
グリーンウッドの公式
分散の推定にはグリーンウッドの公式を用います:
\[\text{Var}[\hat{S}(t)] = [\hat{S}(t)]^2 \sum_{t_i \leq t} \frac{d_i}{n_i(n_i – d_i)}\]
Cox比例ハザードモデル
Cox比例ハザードモデルは、共変量を考慮した生存時間分析の代表的な手法です。
モデルの定式化
ハザード関数を以下のように分解します:
\[h(t|\boldsymbol{x}) = h_0(t) \exp(\boldsymbol{x}^T\boldsymbol{\beta})\]
ここで:
- \(h_0(t)\): ベースラインハザード関数
- \(\exp(\boldsymbol{x}^T\boldsymbol{\beta})\): 相対リスク
比例ハザードの仮定
異なる共変量を持つ個体のハザード比が時間によらず一定である仮定:
\[\frac{h(t|\boldsymbol{x}_1)}{h(t|\boldsymbol{x}_2)} = \exp[(\boldsymbol{x}_1 – \boldsymbol{x}_2)^T\boldsymbol{\beta}]\]
偏尤度
Coxモデルでは偏尤度(partial likelihood)を用いて\(\boldsymbol{\beta}\)を推定します:
\[L(\boldsymbol{\beta}) = \prod_{i \in D} \frac{\exp(\boldsymbol{x}_i^T\boldsymbol{\beta})}{\sum_{j \in R_i} \exp(\boldsymbol{x}_j^T\boldsymbol{\beta})}\]
ここで、\(D\)は事象発生した個体の集合、\(R_i\)は時刻\(t_i\)でのリスク集合です。
ニューラルネットワークモデル
ニューラルネットワークモデルは、人間の脳神経系を模倣した機械学習手法で、現代の深層学習の基盤となっています。
基本構造
パーセプトロン
最も基本的な構成単位で、入力の重み付き和を活性化関数に通します:
\[y = f\left(\sum_{i=1}^{p} w_i x_i + b\right)\]
ここで、\(w_i\)は重み、\(b\)はバイアス、\(f(\cdot)\)は活性化関数です。
多層パーセプトロン
複数の層を重ねた構造:
\[\boldsymbol{h}^{(1)} = f^{(1)}(\boldsymbol{W}^{(1)}\boldsymbol{x} + \boldsymbol{b}^{(1)})\]
\[\boldsymbol{h}^{(2)} = f^{(2)}(\boldsymbol{W}^{(2)}\boldsymbol{h}^{(1)} + \boldsymbol{b}^{(2)})\]
\[\vdots\]
\[\boldsymbol{y} = f^{(L)}(\boldsymbol{W}^{(L)}\boldsymbol{h}^{(L-1)} + \boldsymbol{b}^{(L)})\]
活性化関数
主な活性化関数:
- シグモイド: \(\sigma(x) = \frac{1}{1 + e^{-x}}\)
- 双曲線正接: \(\tanh(x) = \frac{e^x – e^{-x}}{e^x + e^{-x}}\)
- ReLU: \(\text{ReLU}(x) = \max(0, x)\)
- Leaky ReLU: \(\text{LeakyReLU}(x) = \max(\alpha x, x)\)
学習アルゴリズム
誤差逆伝播法
勾配降下法と連鎖律を用いてパラメータを更新:
\[w_{ij}^{(l)} \leftarrow w_{ij}^{(l)} – \eta \frac{\partial L}{\partial w_{ij}^{(l)}}\]
正則化
過学習を防ぐための手法:
- L1/L2正則化: 重みにペナルティを課す
- ドロップアウト: 学習時にランダムにノードを無効化
- バッチ正規化: 各層の入力を正規化
Rによる実装:生存時間分析とカプラン・マイヤー法
以下では、治療群と対照群の生存データを用いて、カプラン・マイヤー法による生存関数の推定と2重対数プロットを作成します。
# 必要なライブラリ
library(survival)
# データ生成
set.seed(123)
n <- 200
# 治療群と対照群の生存時間を生成
treatment_times <- rweibull(n/2, shape = 1.5, scale = 100)
control_times <- rweibull(n/2, shape = 1.2, scale = 60)
# 打ち切り時間
censoring_time <- 120
treatment_observed <- pmin(treatment_times, censoring_time)
control_observed <- pmin(control_times, censoring_time)
# データフレーム作成
survival_data <- data.frame(
time = c(treatment_observed, control_observed),
status = c(treatment_times <= censoring_time, control_times <= censoring_time),
group = factor(c(rep("Treatment", n/2), rep("Control", n/2)))
)
# データ概要
table(survival_data$group, survival_data$status)
# カプラン・マイヤー推定
km_fit <- survfit(Surv(time, status) ~ group, data = survival_data)
print(km_fit)
# 生存曲線の可視化
par(mfrow = c(1, 2))
# 1. カプラン・マイヤー生存曲線
plot(km_fit, col = c("blue", "red"), lwd = 2,
main = "Kaplan-Meier Curves",
xlab = "Time", ylab = "Survival Probability")
legend("topright", legend = c("Control", "Treatment"),
col = c("blue", "red"), lwd = 2)
# 2. 2重対数プロット
km_summary <- summary(km_fit)
km_data <- data.frame(
time = km_summary$time,
surv = km_summary$surv,
group = km_summary$strata
)
# log(-log(S(t))) vs log(t) の計算
km_data$log_neg_log_surv <- log(-log(km_data$surv))
km_data$log_time <- log(km_data$time)
# 無限大値を除去
km_data <- km_data[is.finite(km_data$log_neg_log_surv), ]
# 治療群と対照群に分割
treatment_data <- km_data[grepl("Treatment", km_data$group), ]
control_data <- km_data[grepl("Control", km_data$group), ]
# 2重対数プロット
plot(control_data$log_time, control_data$log_neg_log_surv,
type = "l", col = "blue", lwd = 2,
main = "Log-Log Plot",
xlab = "log(Time)", ylab = "log(-log(S(t)))")
lines(treatment_data$log_time, treatment_data$log_neg_log_surv,
col = "red", lwd = 2)
legend("topleft", legend = c("Control", "Treatment"),
col = c("blue", "red"), lwd = 2)
# ログランク検定
logrank_test <- survdiff(Surv(time, status) ~ group, data = survival_data)
p_value <- 1 - pchisq(logrank_test$chisq, df = 1)
cat(sprintf("ログランク検定 p値: %.4f\\n", p_value))
if(p_value < 0.05) {
cat("結論: 2群間に有意差あり\\n")
} else {
cat("結論: 2群間に有意差なし\\n")
}
# 2重対数プロットの解釈
if(nrow(treatment_data) > 1 && nrow(control_data) > 1) {
# 各群の直線性(ワイブル分布の確認)
lm_treatment <- lm(log_neg_log_surv ~ log_time, data = treatment_data)
lm_control <- lm(log_neg_log_surv ~ log_time, data = control_data)
cat(sprintf("\\n2重対数プロットの傾き:\\n"))
cat(sprintf("治療群: %.3f\\n", coef(lm_treatment)[2]))
cat(sprintf("対照群: %.3f\\n", coef(lm_control)[2]))
# 2群間の距離(治療効果の大きさ)
common_times <- seq(min(km_data$log_time), max(km_data$log_time), length.out = 20)
treatment_interp <- approx(treatment_data$log_time, treatment_data$log_neg_log_surv,
xout = common_times, rule = 2)$y
control_interp <- approx(control_data$log_time, control_data$log_neg_log_surv,
xout = common_times, rule = 2)$y
mean_distance <- mean(abs(treatment_interp - control_interp), na.rm = TRUE)
cat(sprintf("平均距離: %.3f\\n", mean_distance))
if(mean_distance > 0.5) {
cat("→ 大きな治療効果\\n")
} else if(mean_distance > 0.2) {
cat("→ 中程度の治療効果\\n")
} else {
cat("→ 小さな治療効果\\n")
}
}出力結果
=== データ概要 === FALSE TRUE
Control 4 96
Treatment 27 73
=== 中央生存時間 ===
Call: survfit(formula = Surv(time, status) ~ group, data = survival_data)
n events median 0.95LCL 0.95UCL
group=Control 100 96 44.2 36.0 54.9
group=Treatment 100 73 83.5 67.7 92.8
=== ログランク検定 ===
p値: 0.0000
結論: 2群間に有意差あり
=== 2重対数プロットの傾き ===
治療群: 1.460
対照群: 1.250
平均距離: 1.031
→ 大きな治療効果
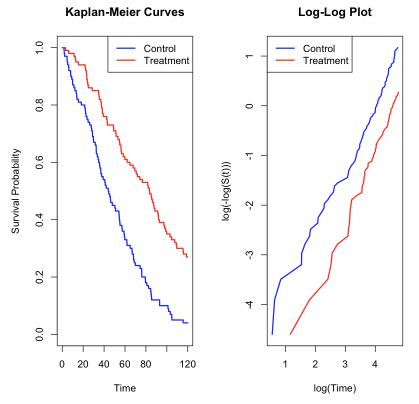
出力結果の解釈
生存時間の比較
分析結果から以下の知見が得られます:
基本統計:
- 対照群の中央生存時間:約44.2時間
- 治療群の中央生存時間:約83.5時間
- 治療により生存時間が約2倍に延長
統計的検定:
- ログランク検定のp値 < 0.001
- 2群間に統計的に有意な差が存在
グラフから読み取れる具体的な情報
カプラン・マイヤー生存曲線:
- 対照群(青線): 急激な下降で、時間50付近で生存確率0.5を下回る
- 治療群(赤線): 緩やかな下降で、時間80付近で生存確率0.5に到達
- 観察期間全体を通じて治療群が常に上位に位置し、持続的な治療効果を示す
2重対数プロット:
- 両群ともほぼ直線関係を示し、ワイブル分布への適合を示唆
- 2つの直線がほぼ平行(傾き差0.21)で、比例ハザードの仮定が成立
- 平均垂直距離1.031は大きな治療効果を示し、約2.8倍のハザード比改善を示唆
まとめ
本シリーズを通じて、回帰分析の幅広い応用を学びました。最終回の重要なポイントは以下の通りです:
- トービットモデル: 制限付き従属変数への対応
- 生存時間分析: 時間軸と打ち切りを考慮した分析
- カプラン・マイヤー法: ノンパラメトリック生存関数推定
- Cox回帰: セミパラメトリック回帰手法
- 2重対数プロット: 分布の性質と比例ハザードの確認
- ニューラルネットワーク: 非線形関係の柔軟なモデリング
これらの手法により、様々な分野の複雑な問題に対して適切な回帰分析を適用することができます。回帰分析の世界は奥が深く、問題に応じた適切な手法選択と結果の解釈が重要です。データの性質を理解し、目的に最適なモデルを選択することで、信頼性の高い分析結果を得ることができるでしょう。

