回帰分析を極める(3/4):質的回帰

これまで連続値を目的変数とする線形回帰について学んできました。しかし、実際の分析では、「病気の有無」「購入の有無」「選択肢の種類」など、カテゴリカルな目的変数を扱うことも多くあります。今回は、そうした質的な目的変数に対する回帰分析手法について詳しく解説します。
目次
一般化線形モデル
一般化線形モデル(Generalized Linear Model, GLM)は、線形回帰を拡張し、様々な確率分布に従う目的変数に対応できるフレームワークです。GLMは以下の3つの要素から構成されます:
- 確率分布(Random Component)
目的変数\((Y)\)が指数型分布族に属する確率分布に従うと仮定します。 - 線形予測子(Systematic Component)
説明変数の線形結合: \[\eta = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_p x_p\] - リンク関数(Link Function)
期待値\((\mu = E[Y])\)と線形予測子\((\eta)\)を結ぶ関数: \[g(\mu) = \eta\]
指数型分布族
指数型分布族は、確率密度関数(または確率質量関数)が以下の形で表される分布族です:
\[f(y; \theta, \phi) = \exp\left(\frac{y\theta – b(\theta)}{a(\phi)} + c(y, \phi)\right)\]
ここで:
- \(\theta\):自然パラメータ
- \(\phi\):尺度パラメータ
- \(a(\cdot)\), \(b(\cdot)\), \(c(\cdot)\):既知の関数
主な指数型分布族には以下があります:
- 正規分布:線形回帰
- ベルヌーイ分布:ロジスティック回帰
- ポアソン分布:ポアソン回帰
- ガンマ分布:ガンマ回帰
ロジスティック回帰モデル
ロジスティック回帰モデルは、二値の目的変数(0または1)を扱う最も代表的な質的回帰手法です。
モデルの定式化
成功確率を\(p = P(Y=1)\)とすると、ロジスティック回帰モデルは:
\[\log\left(\frac{p}{1-p}\right) = \beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p\]
左辺の\(\log\left(\frac{p}{1-p}\right)\)はロジット(logit)と呼ばれ、これがリンク関数となります。
これを\(p\)について解くと:
\[p = \frac{\exp(\beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p)}{1 + \exp(\beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p)}\]
オッズ比
ロジスティック回帰の重要な概念としてオッズ比があります。説明変数\(x_j\)が1単位増加したときのオッズ比は:
\[OR_j = \exp(\beta_j)\]
これは、他の変数を固定したときの「成功のオッズ」の比を表します。
最尤推定
ロジスティック回帰の係数は最尤推定法により求められます。尤度関数は:
\[L(\boldsymbol{\beta}) = \prod_{i=1}^{n} p_i^{y_i}(1-p_i)^{1-y_i}\]
対数尤度を最大化する\(\boldsymbol{\beta}\)を反復的に求めます(通常はニュートン・ラフソン法)。
プロビット回帰モデル
プロビット回帰モデルは、標準正規分布の累積分布関数をリンク関数とする回帰モデルです:
\[P(Y=1) = \Phi(\beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p)\]
ここで、\(\Phi(\cdot)\)は標準正規分布の累積分布関数です。
プロビット回帰とロジスティック回帰の違い:
- ロジスティック回帰:ロジスティック分布(より厚い裾)
- プロビット回帰:正規分布(より薄い裾)
実用上、両者の結果は非常に似ています。
ポアソン回帰モデル
ポアソン回帰モデルは、カウントデータ(非負整数)を目的変数とする回帰モデルです。
モデルの定式化
目的変数\(Y\)がポアソン分布\(Poisson(\lambda)\)に従うとき:
\[\log(\lambda) = \beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p\]
これにより、期待値は:
\[E[Y] = \lambda = \exp(\beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p)\]
ポアソン回帰の解釈
回帰係数\(\beta_j\)の解釈:
- \(\exp(\beta_j)\):説明変数\(x_j\)が1単位増加したときの期待カウントの比(Rate Ratio)
過分散への対処
ポアソン分布では分散=平均ですが、実データでは過分散(分散>平均)が生じることがあります。この場合:
- 準ポアソン回帰:分散の調整
- 負の二項回帰:過分散を許容する分布
その他のGLM
多項ロジスティック回帰
3つ以上のカテゴリを持つ目的変数に対応:
\[P(Y=k) = \frac{\exp(\boldsymbol{x}^T\boldsymbol{\beta}_k)}{\sum_{j=1}^{K}\exp(\boldsymbol{x}^T\boldsymbol{\beta}_j)}\]
順序ロジスティック回帰
順序のあるカテゴリ変数(例:満足度評価)に対応:
\[P(Y \leq k) = \frac{\exp(\alpha_k – \boldsymbol{x}^T\boldsymbol{\beta})}{1 + \exp(\alpha_k – \boldsymbol{x}^T\boldsymbol{\beta})}\]
Rによる実装:高血圧予測のロジスティック回帰
以下では、高血圧の有無を年齢・BMI・喫煙・運動などの要因で予測するロジスティック回帰モデルを構築します。
# シンプルなロジスティック回帰分析
set.seed(123)
n <- 500
# データ生成
data <- data.frame(
age = rnorm(n, 50, 15),
bmi = rnorm(n, 25, 5),
smoking = factor(sample(c("No", "Yes"), n, replace = TRUE)),
exercise = factor(sample(c("No", "Yes"), n, replace = TRUE))
)
# 高血圧の生成(ロジスティック関数)
logit_p <- -3 + 0.05 * data$age + 0.1 * data$bmi +
ifelse(data$smoking == "Yes", 0.8, 0) +
ifelse(data$exercise == "Yes", -0.6, 0)
data$hypertension <- factor(rbinom(n, 1, plogis(logit_p)),
labels = c("Normal", "Hypertension"))
# ロジスティック回帰モデル
model <- glm(hypertension ~ age + bmi + smoking + exercise,
family = binomial, data = data)
# 結果表示
summary(model)
# オッズ比の計算
odds_ratios <- exp(coef(model))
print(round(odds_ratios, 3))
# 予測精度
predicted <- ifelse(fitted(model) > 0.5, "Hypertension", "Normal")
accuracy <- mean(predicted == data$hypertension)
cat(sprintf("予測精度: %.3f\\n", accuracy))
# 効果の可視化
par(mfrow = c(1, 2))
# BMIの効果
bmi_seq <- seq(15, 40, 1)
bmi_pred <- predict(model,
newdata = data.frame(age = 50, bmi = bmi_seq,
smoking = "No", exercise = "No"),
type = "response")
plot(bmi_seq, bmi_pred, type = "l", col = "blue", lwd = 2,
main = "BMI Effect", xlab = "BMI", ylab = "Probability")
# 喫煙・運動の効果
combinations <- expand.grid(smoking = c("No", "Yes"), exercise = c("No", "Yes"))
comb_pred <- predict(model,
newdata = data.frame(age = 50, bmi = 25, combinations),
type = "response")
barplot(comb_pred,
names.arg = c("No Smoking\\nNo Exercise", "Smoking\\nNo Exercise",
"No Smoking\\nExercise", "Smoking\\nExercise"),
col = c("lightgreen", "orange", "lightblue", "red"),
main = "Lifestyle Effects", ylab = "Probability")
出力結果
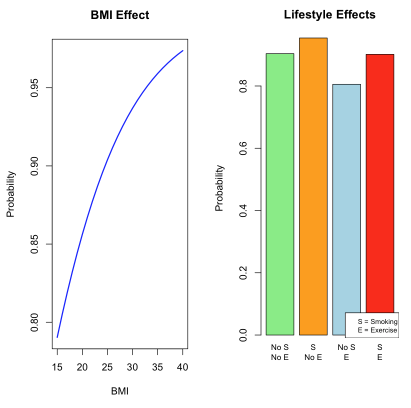
出力結果の解釈
分析結果から以下の知見が得られます:
オッズ比の解釈:
- 年齢: オッズ比 ≈ 1.03 → 年齢が高いほど高血圧リスク増加
- BMI: オッズ比 ≈ 1.10 → BMIが高いほど高血圧リスク増加
- 喫煙: オッズ比 ≈ 2.21 → 喫煙により高血圧リスクが約2.2倍に増加
- 運動: オッズ比 ≈ 0.44 → 運動により高血圧リスクが約半分に減少
可視化結果の解釈:
- BMI効果グラフ:BMIの増加とともに高血圧確率が非線形に上昇
- 生活習慣効果グラフ:「喫煙なし・運動あり」が最も低リスク、「喫煙あり・運動なし」が最も高リスク
モデルの妥当性評価:
- 予測精度: 88.2%という高い精度を達成
- 統計的有意性: すべての変数が有意(p < 0.05)
- AIC: 340.06(モデル比較の指標)
まとめ
質的回帰分析、特に一般化線形モデルについて学びました。重要なポイントを以下に記します:
- 一般化線形モデルは線形回帰を様々な確率分布に拡張
- 指数型分布族が理論的基盤
- ロジスティック回帰は二値分類の標準手法
- プロビット回帰は正規分布ベースの代替手法
- ポアソン回帰はカウントデータに適用
- オッズ比による効果の解釈が重要
- モデル診断と予測性能評価が必須
次回は回帰分析の特殊な応用として、生存時間分析やニューラルネットワークモデルについて学習します。

