Deep IV 徹底解説(2017論文)|深層学習×操作変数で因果推論と反実仮想予測を実現

Deep IV (2017) 論文を図でやさしく解説。深層学習と操作変数法を組み合わせ、因果推論と反実仮想予測を実現する手順と価格戦略・広告最適化への応用例を紹介します。
目次
はじめに
「機械学習モデルをビジネス施策にそのまま使ったら逆効果だった」──そんな経験はないでしょうか。相関を学ぶだけの従来モデルでは、需要ショックや季節要因など観測できない交絡因子が入り込むと、価格と売上の因果関係を誤って推論してしまいます。
2017 年 ICML で発表された “Deep IV” は、この問題を「操作変数法(Instrumental Variables : IV)」とディープラーニングを組み合わせて解決する画期的手法です。
参考文献:
Hartford, J., Lewis, G., Leyton-Brown, K., & Taddy, M. (2017). Deep IV: A flexible approach for counterfactual prediction. In D. Precup & Y. W. Teh (Eds.), Proceedings of the 34th International Conference on Machine Learning (Vol. 70, pp. 1414–1423). PMLR.
https://proceedings.mlr.press/v70/hartford17a.html
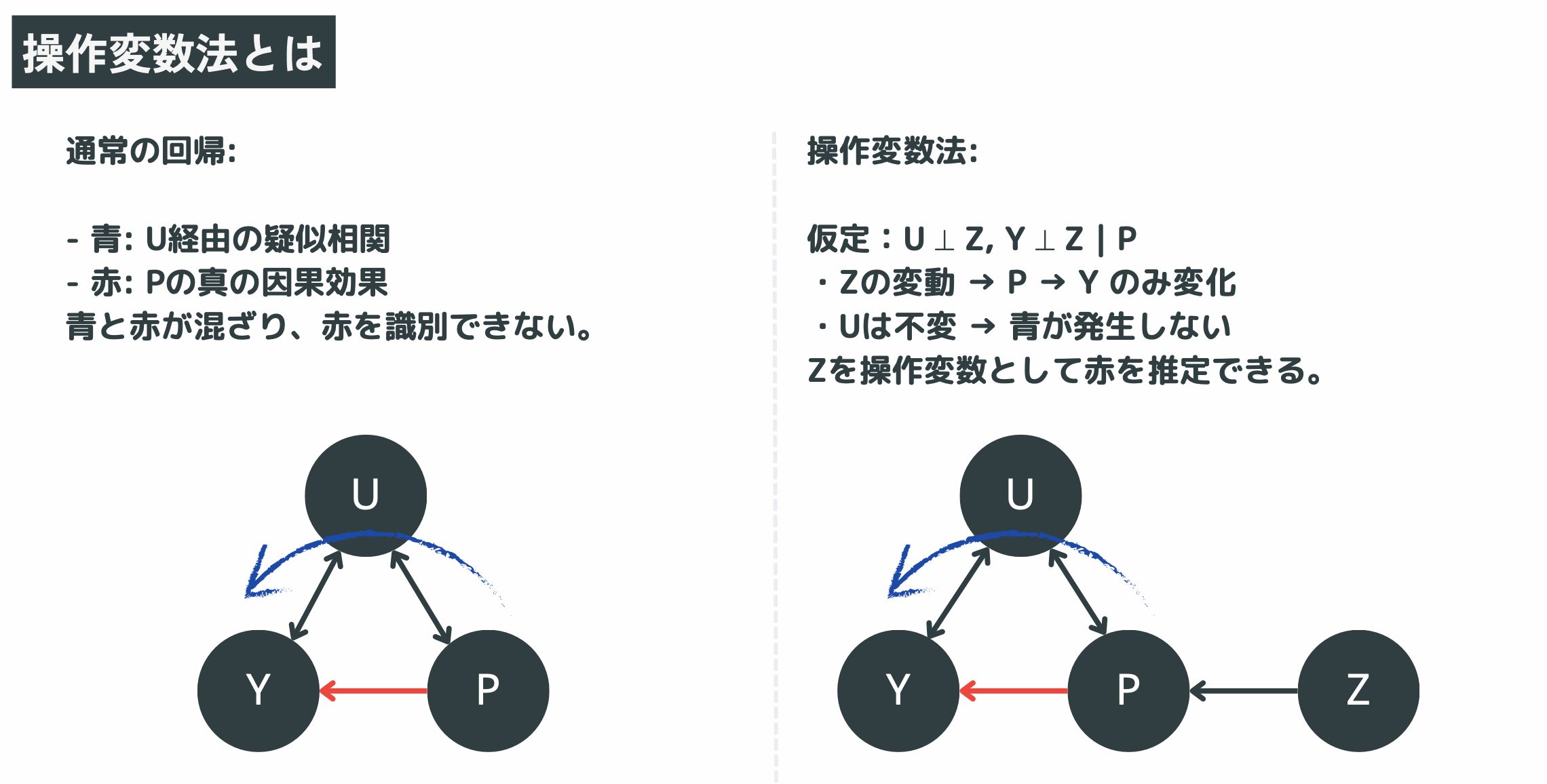
Deep IV とは何か
Deep IV は、内生性(endogeneity)──処置変数 P(たとえば価格)と誤差項 e(需要ショックなど)が相関している状況──でも安定した因果推定を行うために、古典的 IV 推定を 2 段階のニューラルネットワークへ拡張したものです。
・第一段階:操作変数 Z と共変量 X から 「処置 P の条件付き分布」 F(P | X,Z) を推定
・第二段階:上で得た分布から P を何度もサンプリングし、「処置 P が結果 Y に及ぼす反実仮想平均効果」 hθ(P,X) を学習
この2ステップにより、線形 2SLS を超えて非線形かつ個体差のある因果効果を柔軟に表現できます。

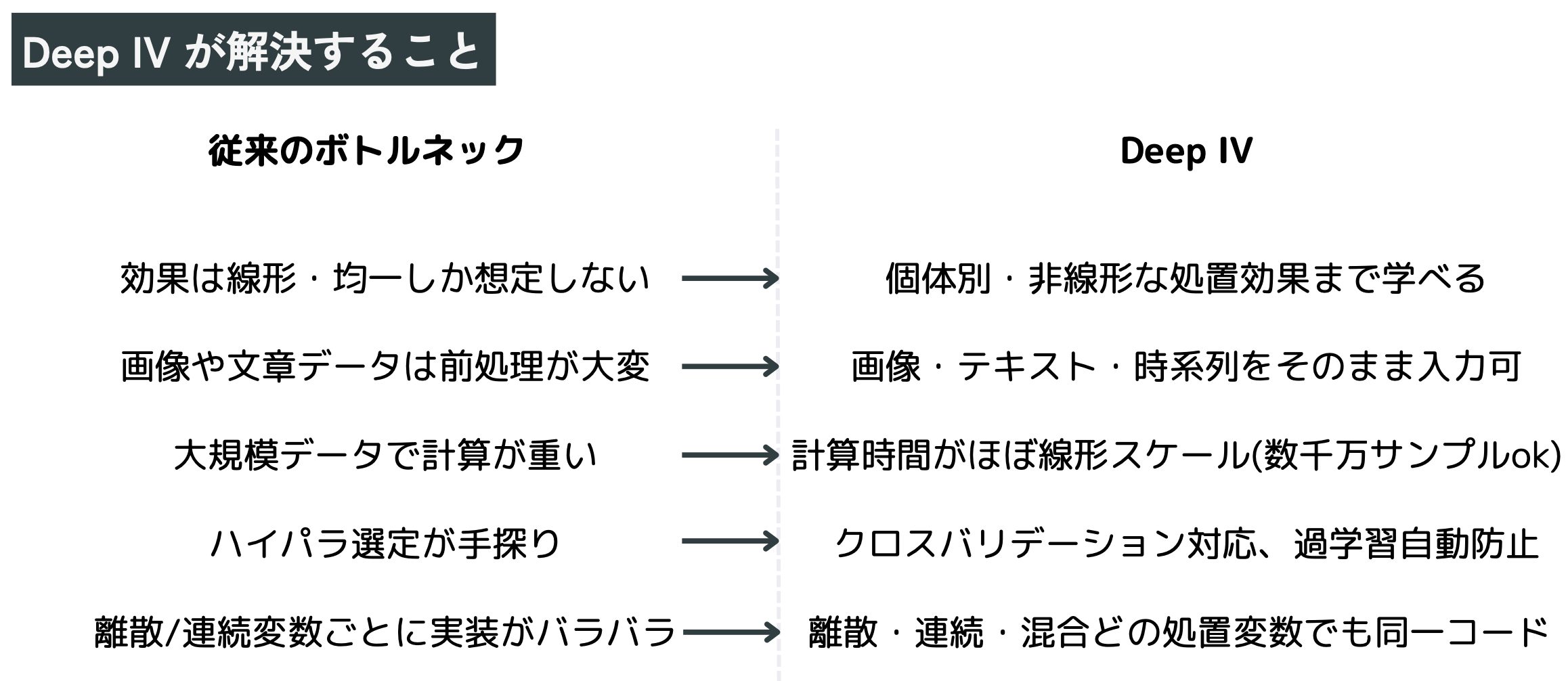
なぜ Deep IV が必要か
航空券の例を考えましょう。ハイシーズンは需要が高いため価格も座席販売数も上がります。単純な回帰モデルは「価格を上げれば売上が伸びる」と誤解しかねません。操作変数として「燃料費 Z」を与えれば、燃料費 → 価格 → 売上 という経路だけが残り、需要ショック e の影響を切り離せます。
しかし従来の IV 推定には
・(1) 線形性・均一効果という強い仮定
・(2) 高次元特徴量へのスケール問題
がありました。Deep IV はニューラルネットを用いることで
・非線形・個体別効果の学習
・画像・テキストなど高次元入力をそのまま扱う
を同時に実現します。
モデルの仕組みと学習テクニック
1. 処置モデル(“くじ箱”を作る)
連続 P なら混合ガウス、離散 P なら Softmax によるカテゴリ分布で F(P | X,Z) を近似。ここで「同じ状況でも起こり得る価格の揺らぎ」をすべて覚えさせます。
2. 結果モデル(くじを引いて平均を取る)
作った分布から B 回サンプリングし、それぞれの (P,X) を入力して Ŷ を出力。モンテカルロ積分で E [Y | do(P),X] を近似し、実際の Y との誤差で θ を更新します。この際サンプルは毎回取り直し、勾配推定のバイアスを防ぎます。
3. 正則化
両ネットの隠れ層には Dropout を適用。多数のサブネットをアンサンブルで学習する効果があり、過学習を抑制します。

シミュレーション結果
低次元設定では、需要ショックと価格の相関 ρ=0.9 の強い内生性下でも Deep IV は 2SLS やカーネル IV を一貫して上回る精度を示しました。データ数が増えるほど誤差が急減し、数万件ではオーダー差の改善が得られます。
高次元設定(顧客タイプを MNIST 画像に置換)でも、検証損失を最小化すると反実仮想 MSE も比例して下がり、画像のような高次元特徴でも因果効果を正確に復元できると確認されました。
実データ応用:検索広告の掲載順位効果
Bing の 2,000 万行に及ぶ検索広告ログを用い、「広告掲載順位がクリック率に与える因果影響」を推定。Bing が実施していた ランダム化実験の ID を操作変数とし、URL やクエリ文字列だけを入力して Deep IV を学習させたところ、
・単純回帰では「順位が 1→2 位でクリック率 70 % 減」と過大評価
・Deep IV では「同 12 % 減」と現実的な効果量
を再現し、従来論文の手作業分析をほぼ自動化しました。
使ってみるためのメモ
・実装:Microsoft EconML に DeepIVEstimator が同梱されており、fit() するだけで利用可能。
・ハイパラ選択:第二段階の検証損失(積分誤差)をそのまま指標にクロスバリデーション。
・データ量の目安:論文のシミュレーションでは、乱択実験に近い精度を得るのに 2 万件程度が必要でした。
・落とし穴:パラメトリックな「価格弾力性」を数式で読めるわけではない/IV の妥当性検証(関連性・排除制約)は依然として不可欠。
まとめ
Deep IV は「操作変数を用いた 2 段階推定」をニューラルネットに乗せ換え、観測データから実験レベルに迫る因果推定を実現した手法です。混合密度ネットワークによる処置分布推定、損失関数内のモンテカルロ積分、Dropout 等の正則化を組み合わせることで、従来の線形 IV が抱えていた非線形性・高次元性の壁を乗り越えました。
広告最適化や価格設定はもちろん、政策評価や A/B テストが難しい領域でも応用可能です。操作変数の設計さえクリアできれば、EconML で手軽に試せるので、興味のある方はぜひ実データで検証してみてください。





