階層クラスタリングをスクラッチで徹底解説(シングルリンク編)

「階層的クラスタリングってライブラリで一発じゃないの?」でも中身を知らないと、なぜそのクラスタになったのか説明できませんよね。
このブログでは、6つの点をもとに、ユークリッド距離とシングルリンク法でデンドログラムを自作する方法をステップバイステップで解説します!
目次
はじめに
「階層的クラスタリングってライブラリで一発じゃないの?」
…たしかに。でも中身を知らないと、なぜそのクラスタになったのか説明できませんよね。
このブログでは、6つの点をもとに、ユークリッド距離とシングルリンク法でデンドログラムを自作する方法をステップバイステップで解説します!
Step 1:データを用意する
今回使う6点の座標は以下のとおり
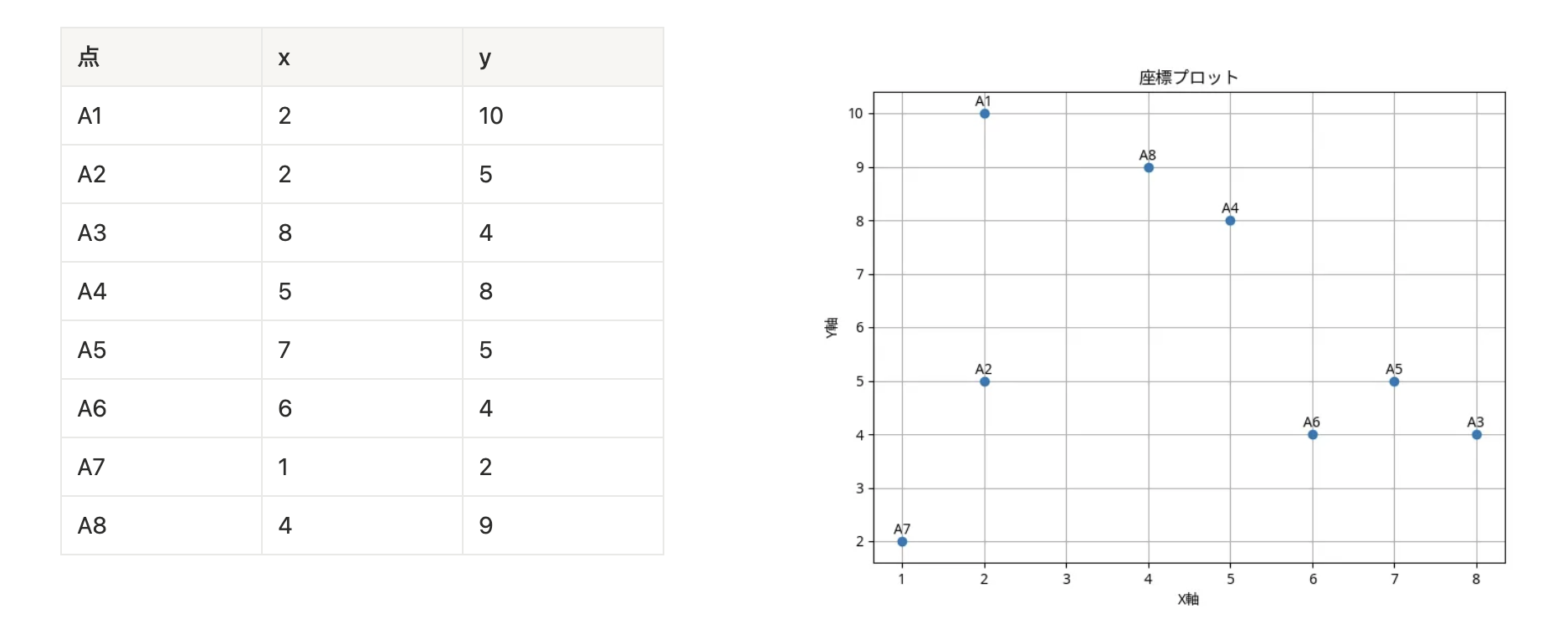
Step 2:ユークリッド距離を計算する
2点間の距離は以下の式で求めます:
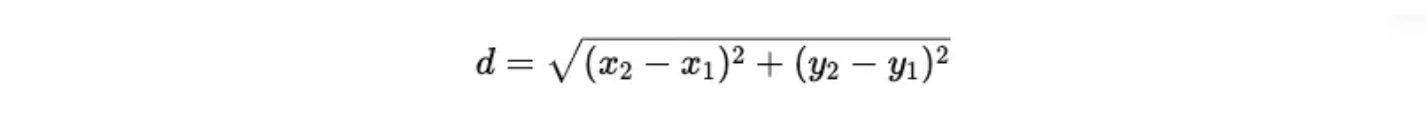
以下に6×6の距離行列を示します(対称なので上三角だけ):
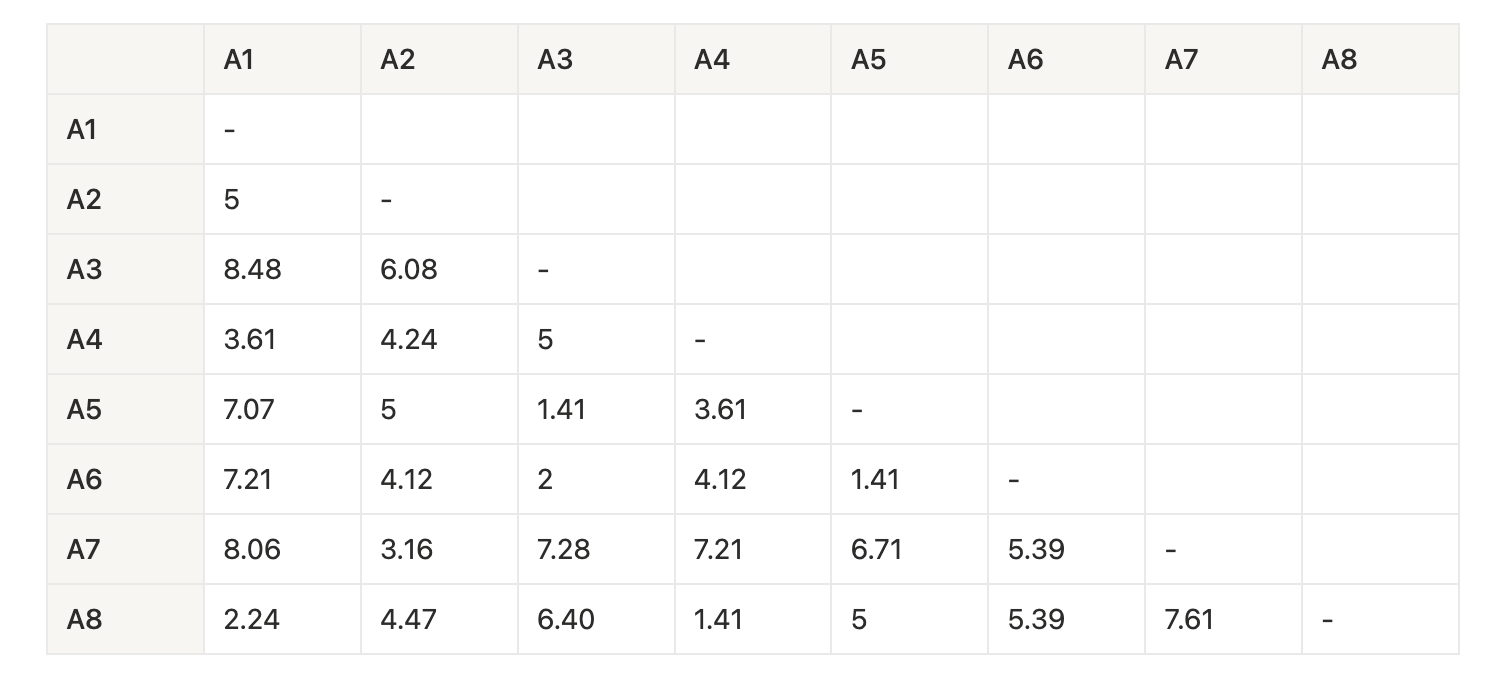
Step 3:最も近い2点をマージ(シングルリンク)
1回目のマージ:
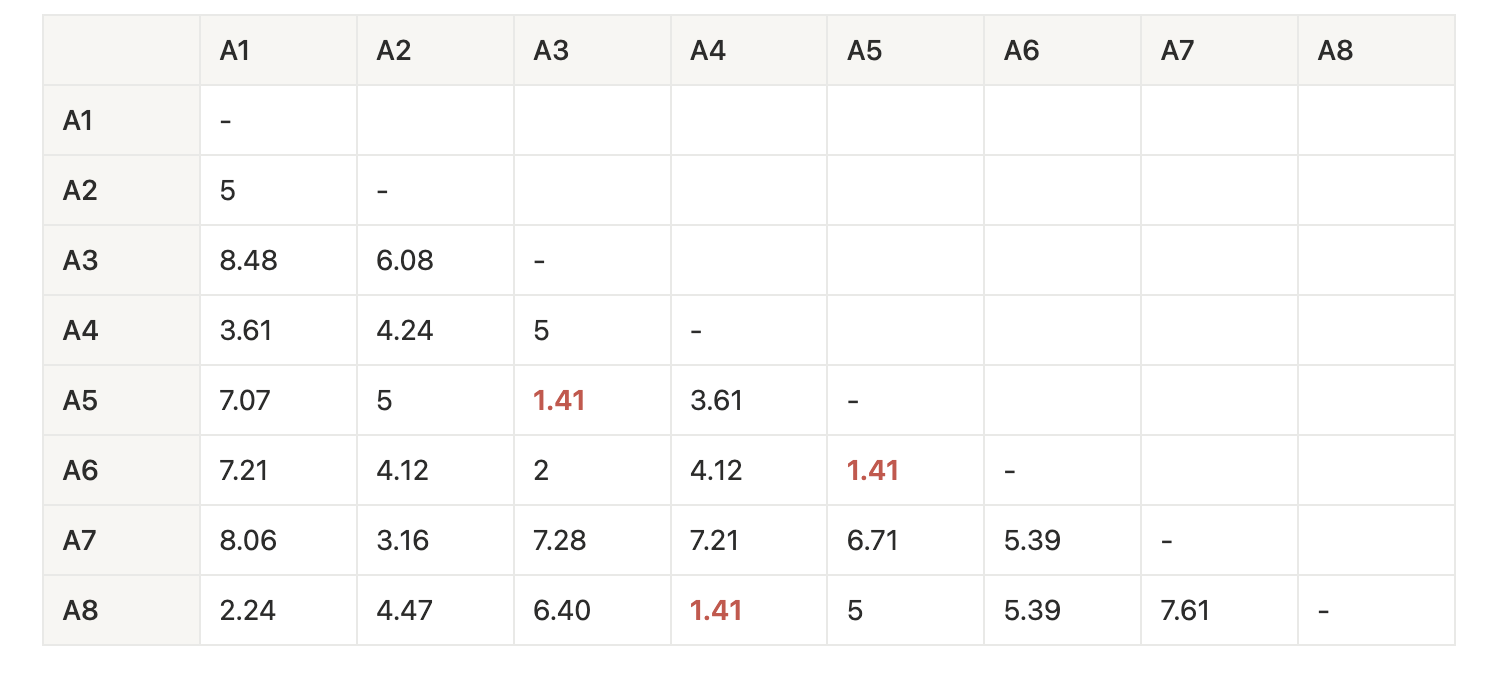
→ 最小距離 1.41 のペアは複数ある(A3-A5-A6, A4-A8)
→ ここでは A1-A5-A6(クラスタ A1-5-6)とA4-A8(クラスタ A4-8)を最初に結合
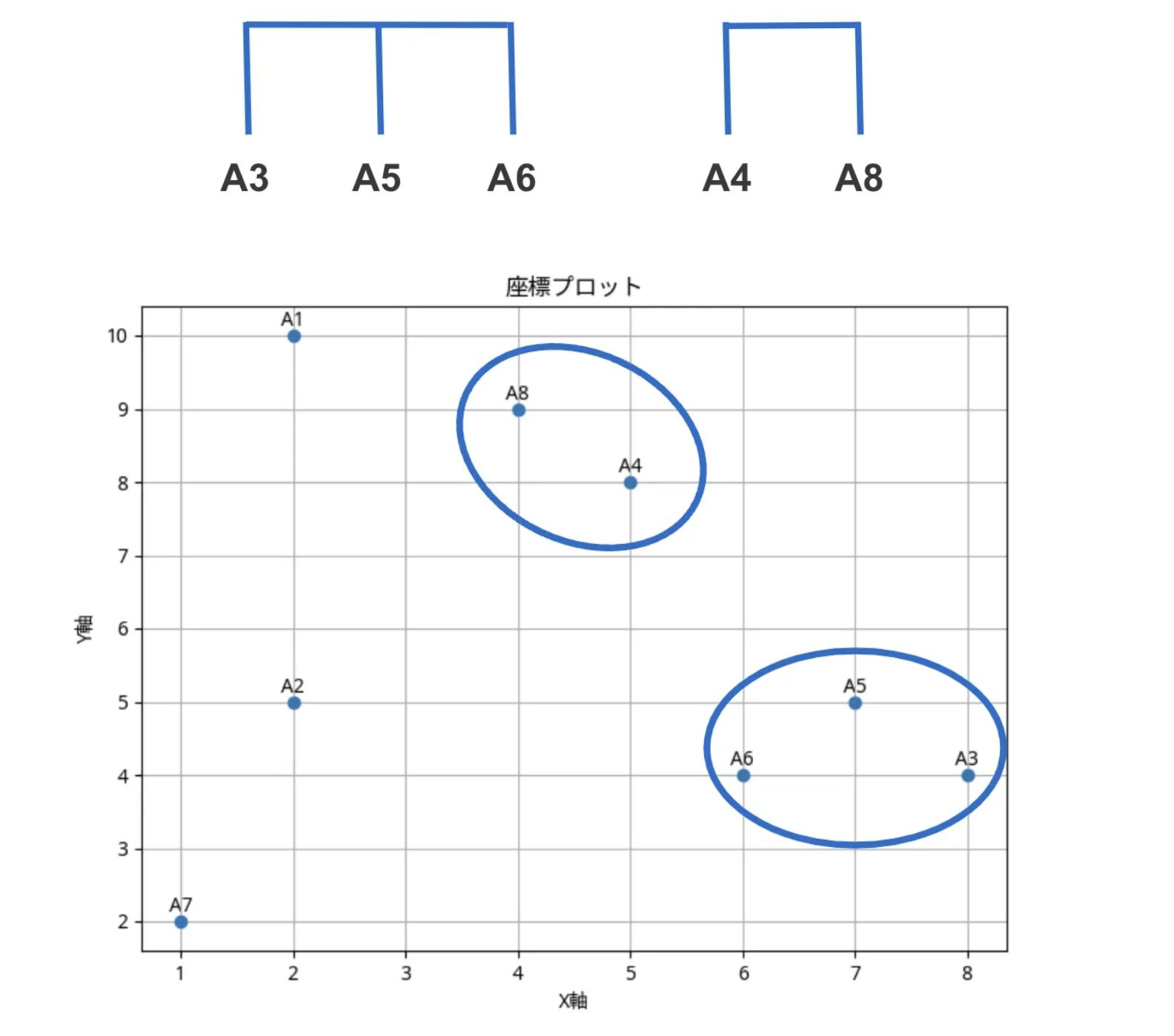
Step 4:距離行列を再計算
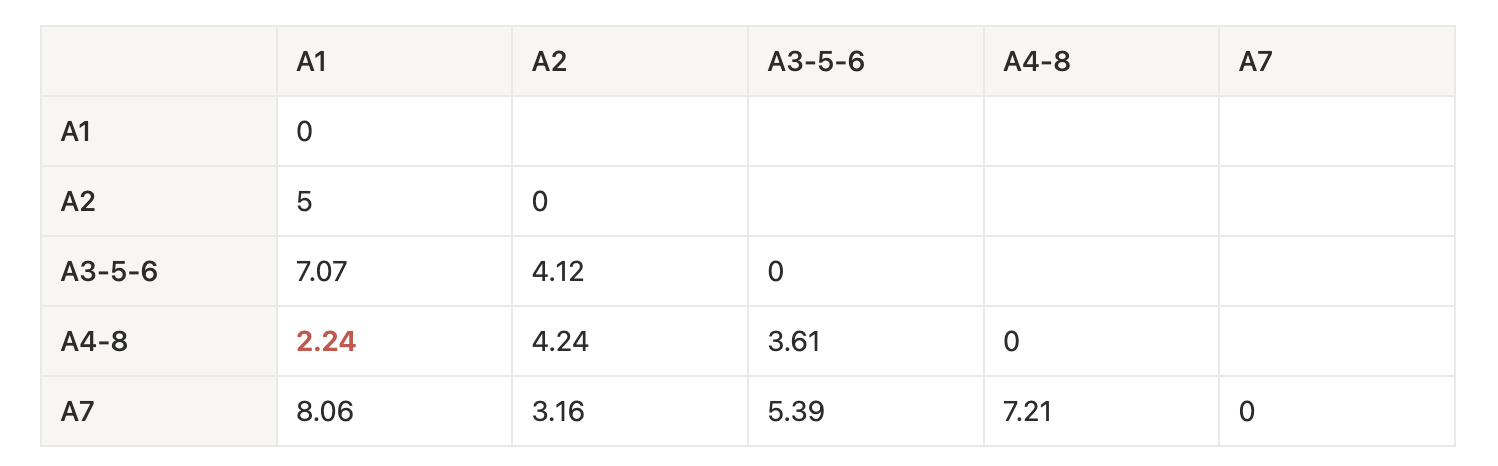
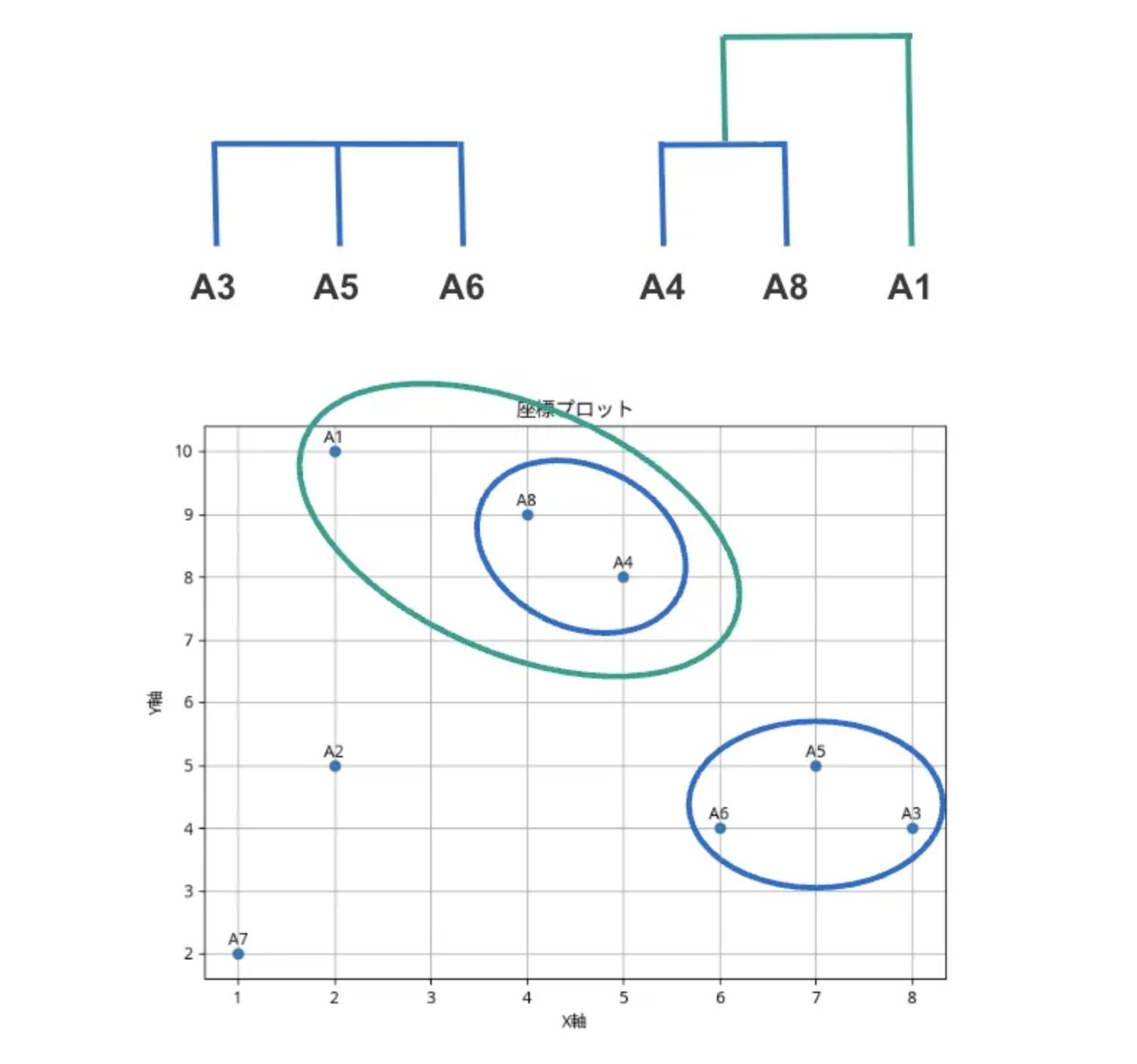
同様に新しくできたクラスタA3-5-6やA4-8と他のクラスターとの距離を最短距離法を計算します。
2回目のマージ:
- MINdist[({A3, A5, A6}, A1) ]= min(dist(A1, A3), dist(A1, A5), dist(A1, A6)) = min(8.485, 7.071, 7.211) = 7.071
- MIN[dist({A3, A5, A6}, A2)] = min(dist(A2, A3), dist(A2, A5), dist(A2, A6)) = min(6.08, 5, 4.123) = 4.123
- MIN[dist({A3, A5, A6}, A7)] = min(dist(A7, A3), dist(A7, A5), dist(A7, A6)) = min(7.28, 6.708, 5.385) = 5.385
- MIN[dist({A4, A8}, {A3, A5, A6})] = min(dist({A3, A5, A6}, A4), dist({A3, A5, A6}, A8)) = min(3.605, 4.9) = 3.605
3回目のマージ:
MIN[dist(A1, {A4, A8}), A7] = MIN[dist(A1, A7), dist({A4, A8}, A7)] = min(8.062, 7.21) = 7.21
MIN[dist(A1, {A4, A8}), (A3, A5, A6)] = MIN[dist(A1, {A3, A5, A6}), dist({A4, A8}, {A3, A5, A6})] = MIN[dist(A1, A3), dist(A1, A5), dist(A1, A6), dist({A4, A8}, A3), dist({A4, A8}, A5), dist({A4, A8}, A6)] = … = min(7.071, 3.605) = 3.605
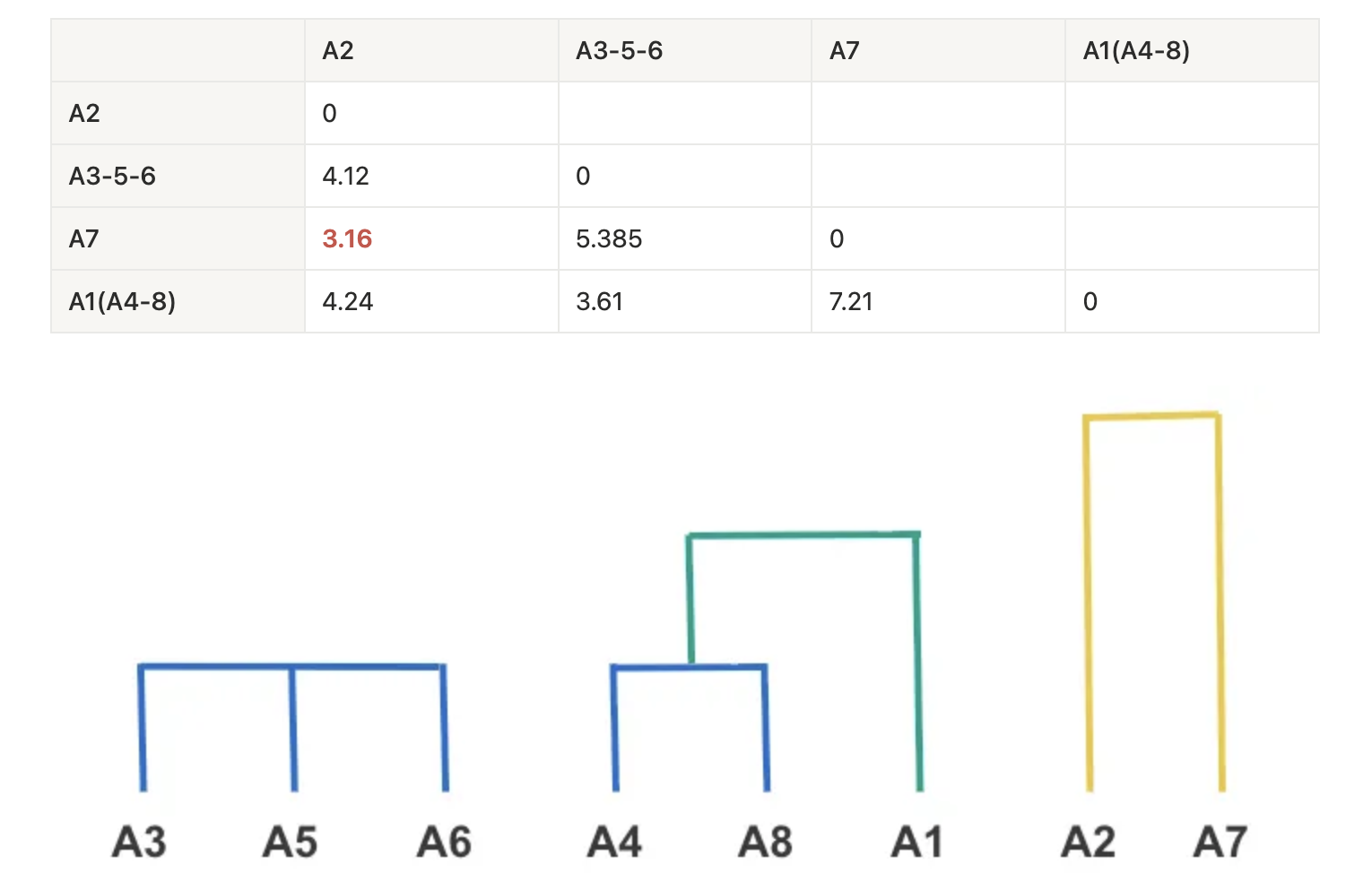
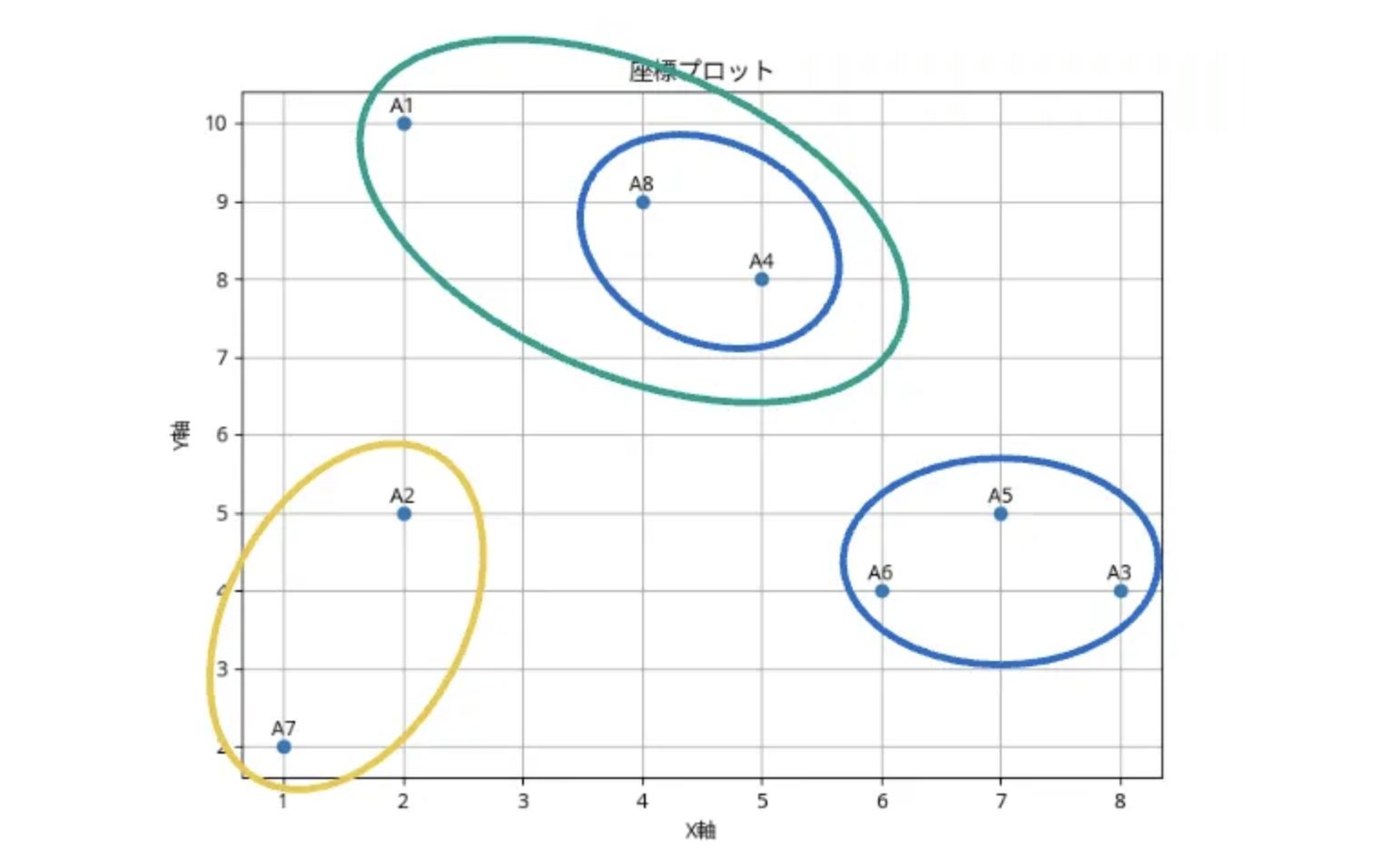
4回目のマージ:
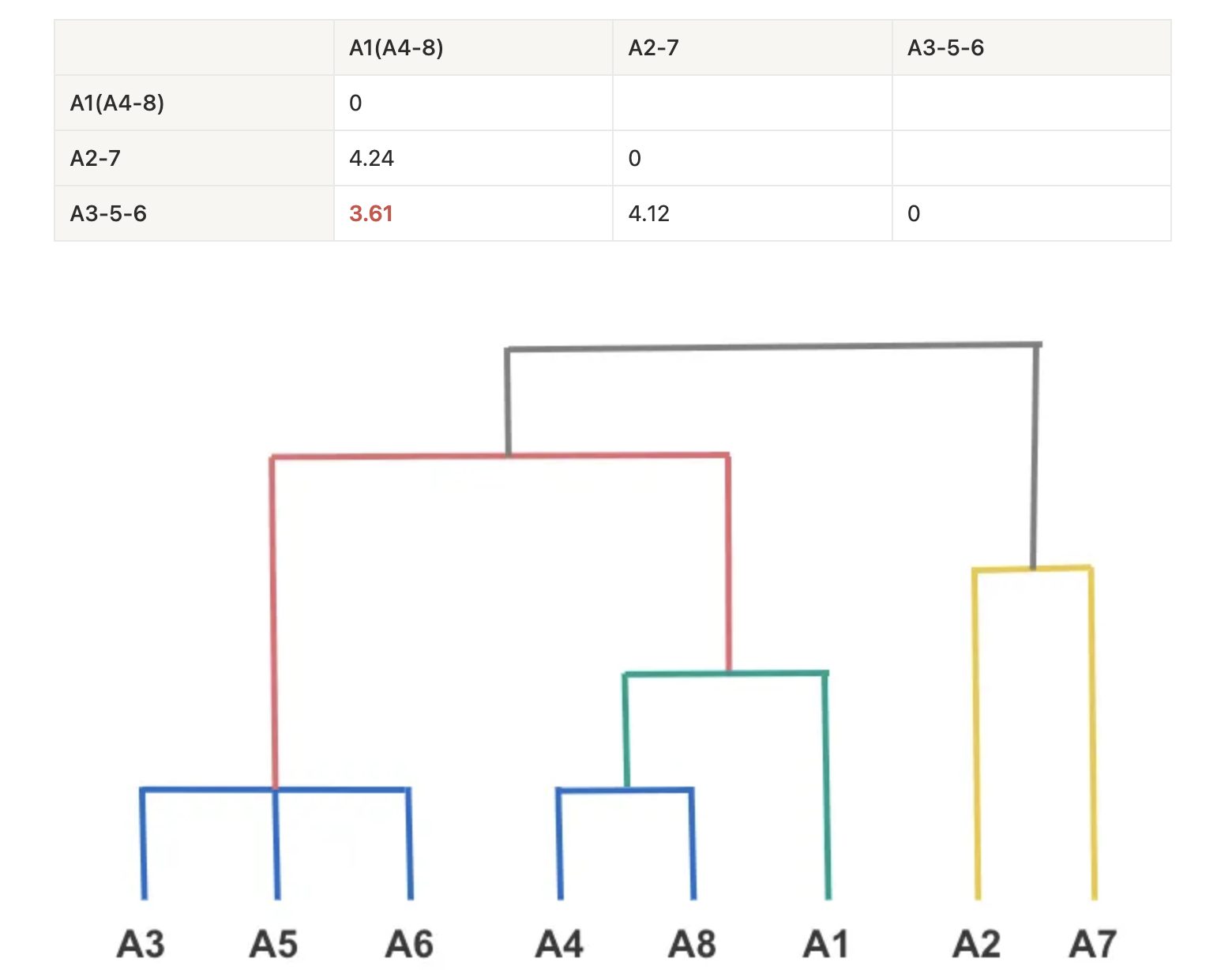
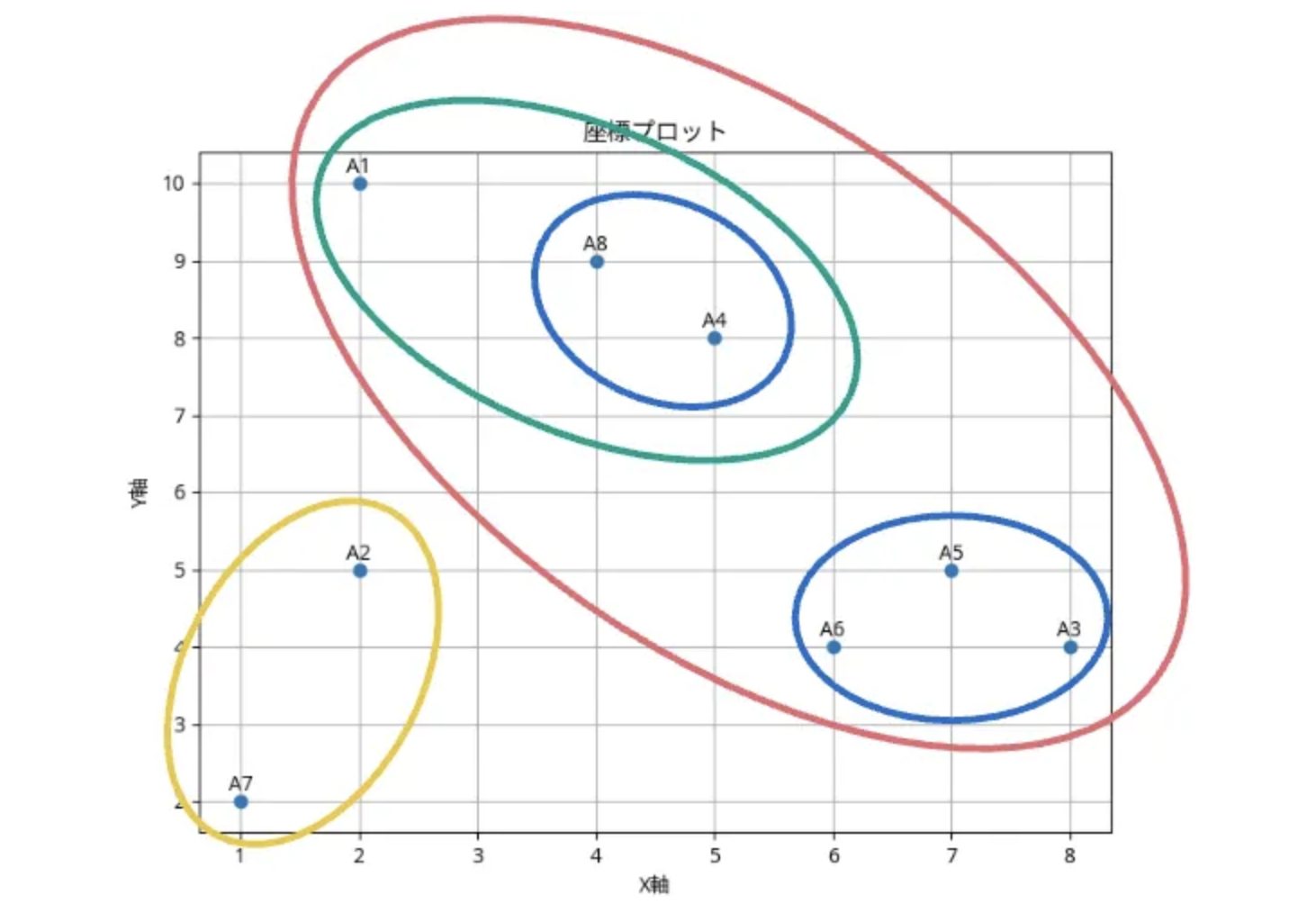
Step 5:クラスタ数を決めるには?
このデンドログラムをどこで切るかがポイント。
- 高さ = 1.0 → 3クラスタ(A3-5-6, A1{A4-8}, A2-7)
- 高さ = 4.2 → 2クラスタ({(A3-5-6), A1(A4-8)}, A2-7)
- 高さ = 8.5 → 1クラスタ(すべて統合)
おわりに
この記事では、手計算による階層クラスタリング(凝集型、最短距離法)の具体的な計算例をステップバイステップで解説しました。初期のデータポイントから距離行列を作成し、最も近いクラスターを繰り返し結合していくことで、最終的に全てのデータポイントが1つのクラスターにまとまる過程を追うことができました。
この計算例を通して、階層クラスタリングの基本的なロジックと、最短距離法がクラスター間の距離にどのように影響するかを理解いただけたかと思います。






