Data Driven Knowledgebase

一言で言えば、数理最適化とは「与えられた制約条件の中で、最も良い結果（ベストな解）を数学的に導き出す手法」のことです 。

ここで言う「最も良い結果」とは、あらかじめ設定した「目的関数」と呼ばれるスコアを、最大化（例：利益、満足度）または最小化（例：コスト、時間）することを指します 。

私たちの生活の中にある具体的な例を見てみましょう。

・最短経路問題（時間の最小化） 例えば、乗り換え案内アプリで「新宿から浜松町まで一番早く着くルート」を検索するとします 。これは、「移動にかかる時間」というスコアを最小化する問題です。

・満足度の最大化（カロリーの例） 少しユニークな例ですが、「1000円の予算内で、摂取カロリーを最大にするランチの組み合わせ」を考えるとします 。

サラダチキン（200円, 150kcal）

ラーメン（600円, 500kcal）

パスタ（400円, 350kcal）

この場合、「予算1000円」が制約条件で、「摂取カロリー」が最大化したいスコア（目的関数）になります。

ビジネスの現場では、限られた在庫や人員で工場の売上を最大化する「生産計画」や、相性を考慮した最適な「クラス分け・チーム編成」など、様々な場面で活用されています 。

扱うデータの性質によって、数理最適化は大きく2つに分けられます 。

・連続最適化問題: 「1.98kg」や「3.5時間」のように、変数が連続的な実数値をとる問題です 。

・離散最適化問題: 「人数」や「商品の個数」のように、変数が「1個、2個」といった飛び飛びの整数値しかとれない問題です 。

数理最適化のイメージを掴むために、最も基本的で代表的な「線形計画問題」を例に考えてみましょう 。これは、制約条件と目的関数がすべてシンプルな一次式（直線的な関係）で表される問題です 。

以下の問題を考えてみます 。

• 制約条件（守るべきルール）:
  
  
  
  
  • 2x1 + 3x2 ≤ 8
  
  
  • 4x1 + 3x2 ≤ 10
  
  
  • x1 ≥ 0, x2 ≥ 0 （x1, x2はマイナスにならない）
  
  
  
  


• 目的関数（最大化したいスコア）:
  
  
  
  
  • z = x1 + x2 の最大化
  
  
  
  

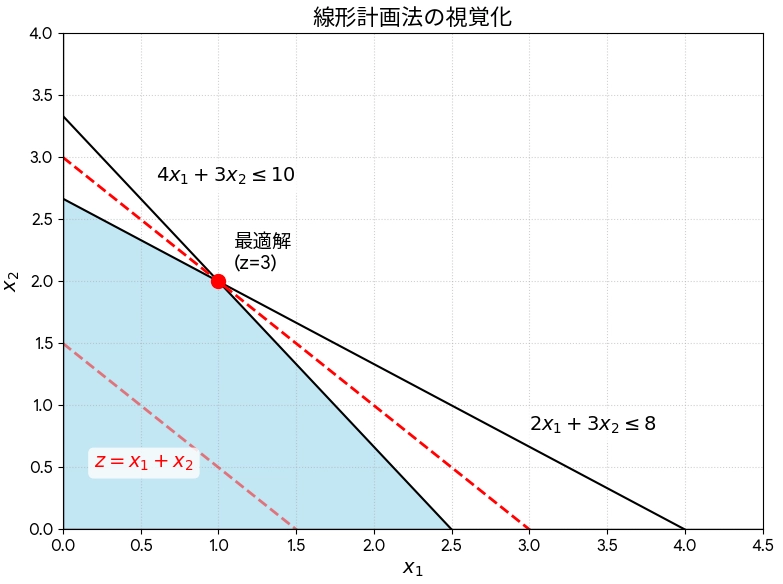
この問題をグラフで視覚的に解くと、以下のようになります。

 

 

【グラフの解説】

実行可能領域（青色の部分）: 2つの制約条件の式と、x1, x2が0以上という条件をすべて満たすエリアです。このエリア内のどこかに答えがあります。

目的関数の直線（赤い点線）: z = x1 + x2 の値を表す直線です。この直線を動かしていくと、zの値（スコア）が変化していきます。

最適解（赤点）: 実行可能領域の中で、目的関数が最も最大化している点です。グラフから、2つの制約を表す直線の交点である (x1=1, x2=2) が最適解であり、その時の最大スコアは z=3 となることが分かります。

このように線形計画問題の解を求めていきます。

今回は、数理最適化の基礎として、その定義や分類、そして基本的な線形計画問題の解き方を紹介しました 。世の中の多くの複雑な問題も、実はこの線形計画問題に帰着させて考えることができます 。

現在のデータ分析の現場では、機械学習による「予測」が注目されがちです。しかし、予測した結果を元に「次にどのようなアクションを取るべきか」という最適な意思決定を行うためには、数理最適化が不可欠です。これもまた、数字に基づいた重要なデータドリブンなアプローチと言えるでしょう 。

実際のビジネス現場では、より複雑な条件や膨大なデータを扱うため、専用のアルゴリズムや「ソルバー」と呼ばれる計算ソフトを活用します 。もし興味を持たれた方は、さらに深い数理最適化の世界を探求してみてください 。